Engineering Physics

Lab Report #5

PH - 261 - 11

Newton II - Atwood's Machine



Andy Buettner

Mr. Huttlin


Objective


The Objective of this lab is to study the validity of Newton's third law, Force = Mass * Acceleration, by studying Atwood's Machine.


Materials


  1. Timer

  2. Atwood's Machine

  3. Complete set of masses

  4. Measuring device


Procedure


I) Part 1:


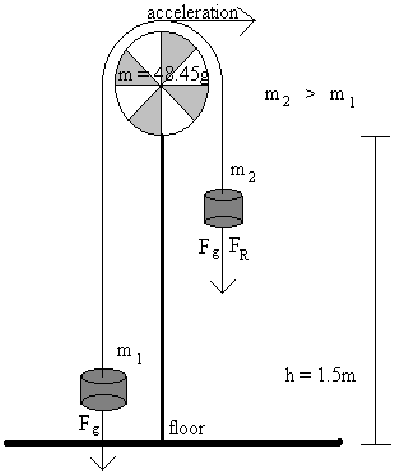
  1. Measure the height, of the system, the mass of each weight tray, and the mass of the pulley system.

  2. Place 1040g of mass on each side.

  3. Remove 10g of mass from one side and place it on the other.

  4. Move the more massive end to the top of the machine.

  5. Time the time it takes for the more massive end to fall to the ground.

  6. Repeat step 5 four additional times and record the results.

  7. Repeat steps 4 through 6 three additional times.


II) Part 2:


  1. Remove all masses from the system.

  2. Place 30g of mass on one side but not the other.

  3. Place 400g of mass on each side of the system

  4. Move the more massive end to the top.

  5. Allow the more massive end to fall and record the time it takes.

  6. Repeat step 5 four additional times.

  7. Repeat steps 4 through 6 three additional times adding an additional 200g of mass to each side.


Data


I) Table 1: Results for 1050g / 1030g mass combination.


Trial #:

1

2

3

4

Average

Time:

6.02s

5.73s

5.82s

6.06s

5.91s


II) Table 2: Results for 1060g / 1020g mass combination.


Trial #

1

2

3

4

5

Average

Time:

4.19s

4.13s

4.18s

4.20s

4.14s

4.17s


III) Table 3: Results for 1070g / 1010g mass combination.


Trial #:

1

2

3

4

5

Average

Time:

3.40s

3.55s

3.65s

3.40s

3.39s

3.48s


IV) Table 4: Results for 1080g / 1000g mass combination.


Trial #:

1

2

3

4

5

Average

Time:

2.89s

2.89s

2.95s

3.03s

3.07s

2.96s


V) Table 5: Average Results for part 1.


Mass of Left:

1050g

1060g

1070g

1080g

Mass of Right:

1030g

1020g

1010g

1000g

Average Time:

5.19s

4.17s

3.48s

2.96s


VI) Diagram 1: Illustration of Atwood's Machine.


VII) Table 6: Results for 400g / 430g mass combination.


Trial #:

1

2

3

4

5

Average

Time:

3.03s

2.93s

3.36s

3.43s

3.08s

3.17s


VIII) Table 7: Results for 600g / 630g mass combination.


Trial #:

1

2

3

4

5

Average

Time:

3.77s

3.83s

3.75s

3.70s

3.75s

3.76s


IX) Table 8: Results for 800g / 830g mass combination.


Trial #:

1

2

3

4

5

Average

Time:

4.21s

4.37s

4.30s

4.34s

4.21s

4.29s


X) Table 9: Results for 1000g / 1030g mass combination.


Trial #:

1

2

3

4

5

Average

Time:

4.84s

4.90s

4.87s

4.81s

4.77s

4.84s


XI) Table 10: Average Results for part 2.


Mass of Left:

430g

630g

830g

1030g

Mass of Right:

400g

600g

800g

1000g

Average Time:

3.17s

3.76

4.29

4.84


Analysis


% Deviation for part 1:


Mass of left (heavier) side

Trial #

1050g

1060g

1070g

1080g

1

1.86%

.96%

2.30%

2.36%

2

3.05%

.96%

2.01%

2.36%

3

1.52%

.24%

4.89%

.34%

4

2.54%

.72%

2.30%

2.36%

5


.72%

2.59%

3.72%


% Deviation for Part 2:


Mass of left (heavier) side
Trial #

430g

630g

830g

1030g

1

4.42%

.27%

1.86%

0%

2

7.57%

1.86%

1.86%

1.24%

3

5.99%

.27%

.23%

.62%

4

8.20%

1.60%

1.17%

.62%

5

2.84%

.27%

1.86%

1.45%

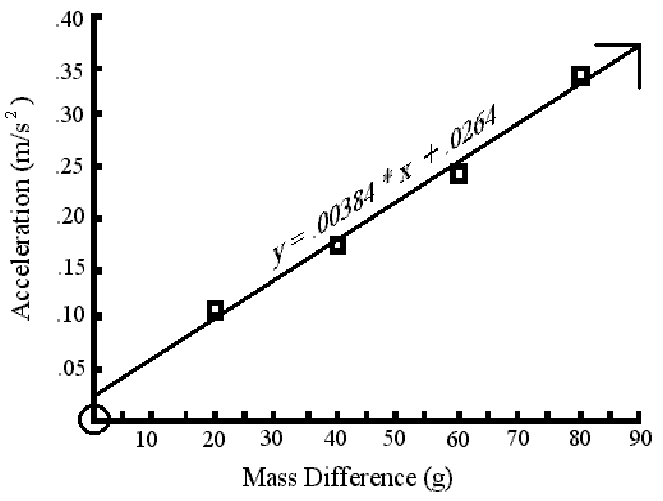
Graph of Mass difference vs. Acceleration for part 1:


Zero acceleration


When the mass difference is 6.88g or less the acceleration will be 0.

Using this value, the force of friction is: .364N


Conclusions


From this lab one could conclude that Newton's third law is correct. The force on an object is dependant on both of the key factors, mass, and acceleration. I would like to comment that parts of this lab were unclear as to what measurements and calculations were required. As a result all measurements were provided for additional interpretation.


Answers to Lab Questions


1) Q: Derive an equation for the acceleration of a pulley system that accounts for a mass less, and frictionless system except for the masses of each individual side.

A: For m1 < m2: a = g * m2 / (m1 + m2).


  1. Q: If m1 is chosen to be 93% of m2, what percent of freefall should the system have?

A: 51.8%


3) Q: Why would the tensions for T1 and T2 not be the same?

A: The tensions would be different because there would be a friction force in the pulley that would have to be accounted for. Additionally, some of the tension would have to be used as torque in order to allow the pulley to accelerate.


4) Q: What is the total effective mass undergoing an acceleration?

A: The entire system is being accelerated in some way so the mass would be that of the entire system: 2229g.


5) Q: What is the driving force producing the acceleration?

A: The driving force is the gravitational constant (g) multiplied by the heavier side's mass.


6) Q: Why were m1 and m2 chosen so that their mass was at least 1Kg?

A: The larger the mass of the entire system is, the less the acceleration will be.


7) Q: Why was the mass difference chosen to be so small?

A: The smaller the mass difference, the less the acceleration would be. If the acceleration were large, accurate measurements could not be taken.