EE - 456 / E01 spring 2003

Advanced Communications Theory

Professor: Arida

Submitted By:

Andrew Buettner

Partner:

Steven Thomas

Lab #4: Spectral Measurement

Saturday, April 26, 2003

Table Of Contents

1) Cover Page 1

2) Table of Contents 2

3) Objective 4

4) Components Used 4

5) Procedures 4

6) Lab Data / Results 5

1) Diagram 1 5

2) Diagram 2 6

3) Diagram 3 6

4) Diagram 4 7

5) Diagram 5 7

6) Diagram 6 8

7) Diagram 7 8

8) Diagram 8 9

9) Diagram 9 9

10) Diagram 10 10

11) Diagram 10 10

12) Diagram 10 11

13) Diagram 10 11

14) Diagram 10 12

15) Diagram 10 12

16) Diagram 10 13

17) Diagram 10 13

18) Diagram 10 14

19) Diagram 10 14

20) Diagram 10 15

21) Diagram 10 15

7) Answers to Lab Questions 16

8) Conclusions 16

Table Of Contents (Continued)

9) Attachments 16

Objective

This lab will investigate the use of the Fast Fourrier Transform to derive the spectra of an arbitrary signal in discrete time. For some of the transforms, windowing will be employed to reduce spectral leakage.

Components Used

1) Computer running Octave

2) Digital sampling board

3) Oscilloscope #

4) Function Generator #

Procedures

1) Generate a sixteen sample sine wave where w = w_s/4 using "x=cos(2*ip*n/4);" where "n=0:15"

2) Plot the function.

3) Using fft, generate and plot X, the Fourrier transform of the signal.

4) Repeat steps 2 and 3 for frequencies w_s/8, w_s/16, and w_s/2.

5) Describe the difference for the last case where w = w_s/2.

6) Generate a signal where w = 2.1*p/4.

7) Repeat steps 2 and 3.

8) Illustrate the spectral leakage.

9) Apply a Hamming window to the time-domain signal using "x2=x.*hamming(16);"

10) Plot the new signal.

11) Generate and plot the spectrum of the new signal.

12) Explain the difference.

13) Set the function generator to generate a 25KHz signal.

14) Enter command "ssrat(100000)"

15) Enter command "x=ad(100);" to capture 100 samples.

16) Find and plot the resulting spectrum, it should be similar to the spectrum of the signal where w = w_s/4.

17) Generate a signal using the following commands:

a) X=zeros(1,16);

b) X(2) = 1;

c) X(16)=1;

d) x=real(ifft(X));

18) Plot X.

19) Plot x.

20) Realize the signal using the following commands:

a) ssrat(100000)

b) x=8192.*x;

c) da(x)

21) Record the resulting waveform.

22) Find the frequency of the resulting signal, it should be near 6KHz.

23) Create an array X that contains the spectrum to an AM signal where w_c = w_s/8, w_m = w_s/64, and m=.75.

24) Plot the spectra.

25) Generate a time-domain signal from the spectra.

26) Plot the time-domain signal.

27) Realize the signal.

28) Record the resulting waveform.

Lab Data / Results

1) Diagram 1: w_s/4 time-domain signal:

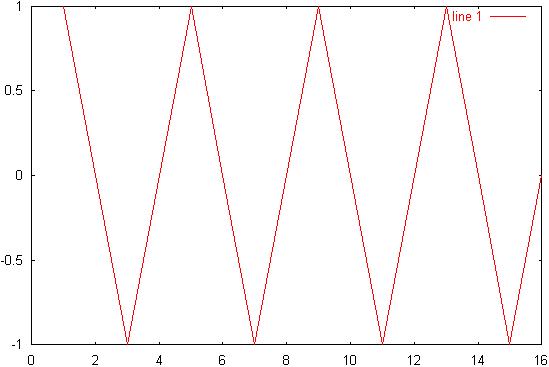
2) Diagram 2: w_s/4 spectrum:

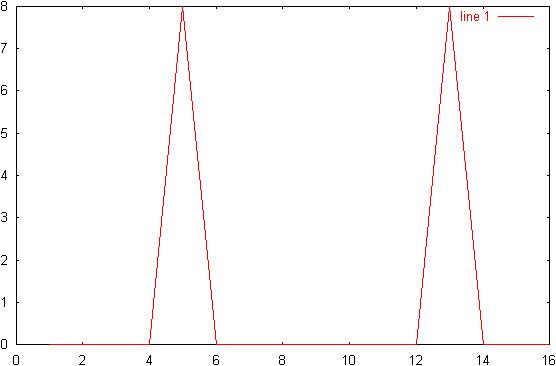
3) Diagram 3: w_s/8 signal:

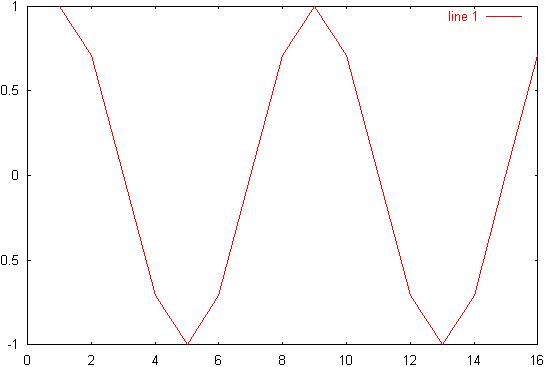
4) Diagram 4: w_s/8 spectrum:

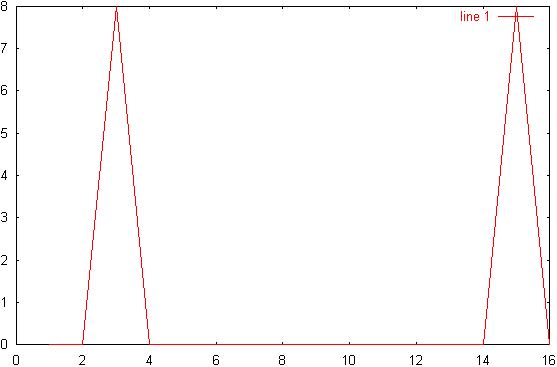
5) Diagram 5: w_s/16 signal:

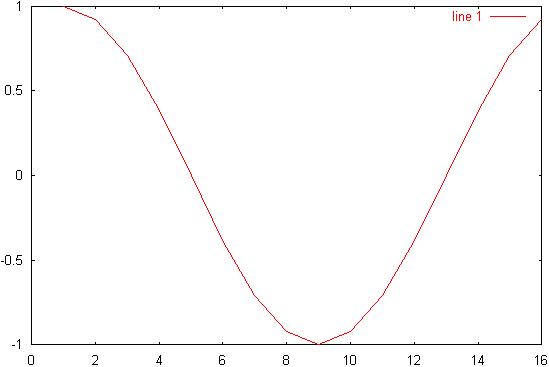
6) Diagram 6: w_s/16 spectrum:

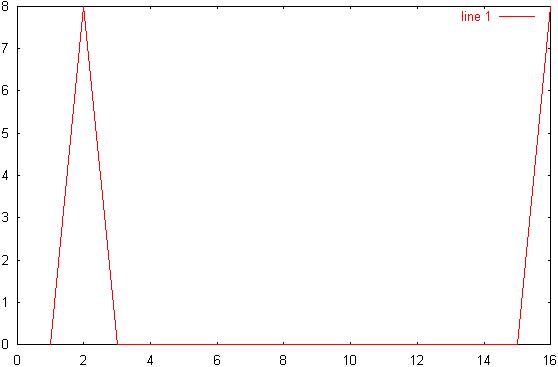
7) Diagram 7: w_s/2 signal:

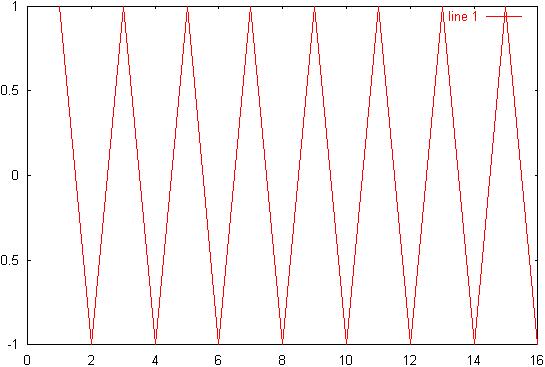
8) Diagram 8: w_s/2 spectrum:

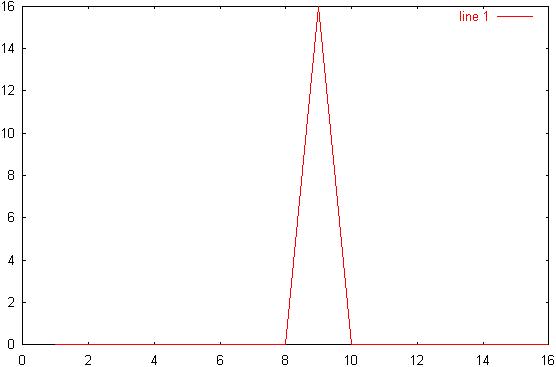
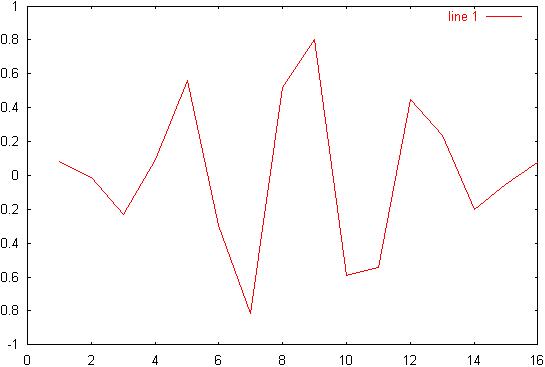
9) Diagram 9: 2.1p/4 signal:

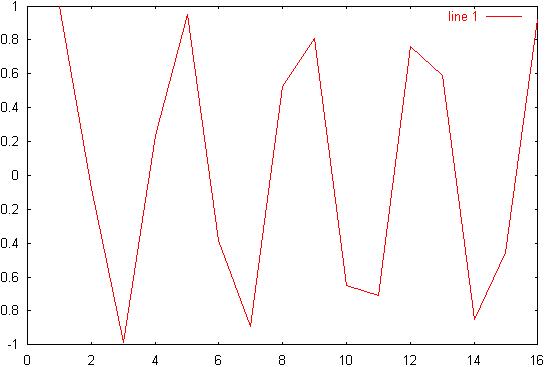
10) Diagram 10: 2.1p/4 spectrum:

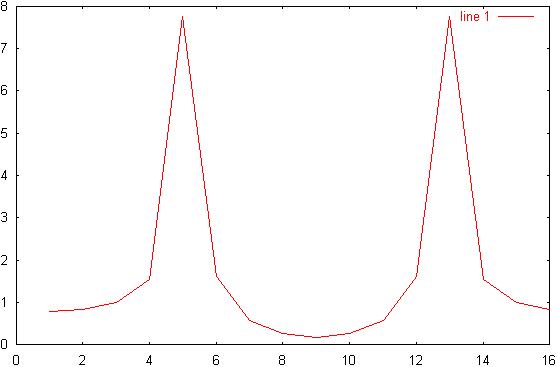
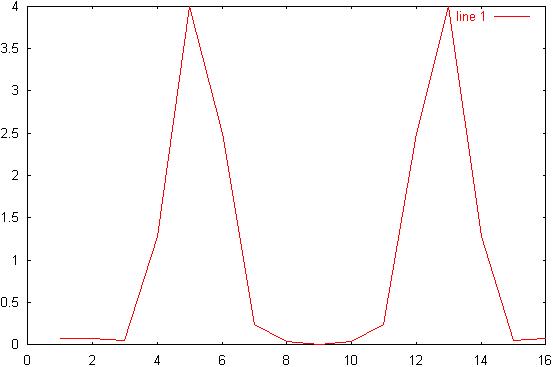
11) Diagram 11: Hamming signal:

12) Diagram 12: Hamming signal spectrum:

13) Diagram 13: w_s/4 real signal

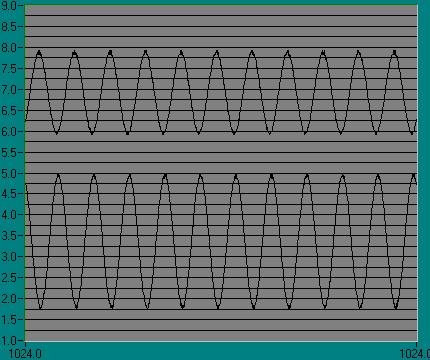
14) Diagram 14: w_s/4 captured signal:

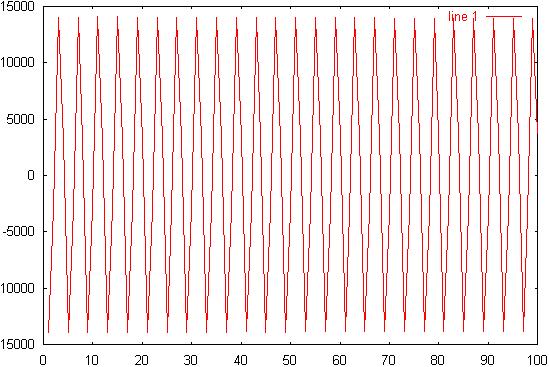
15) Diagram 15: w_s/4 signal spectrum:

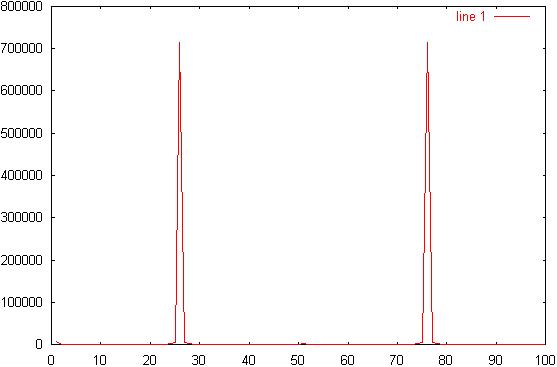
16) Diagram 16: Generated signal spectrum:

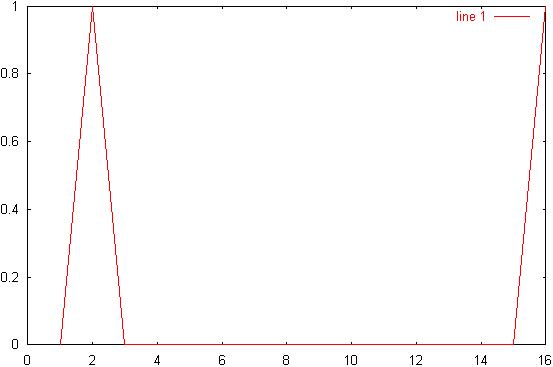
17) Diagram 17: Generated signal:

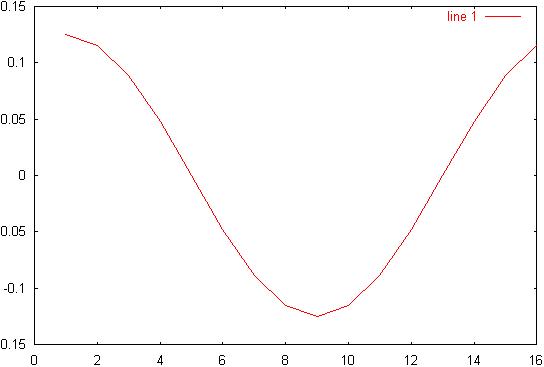
18) Diagram 18: Realized signal: (F Z 1.5KHz)

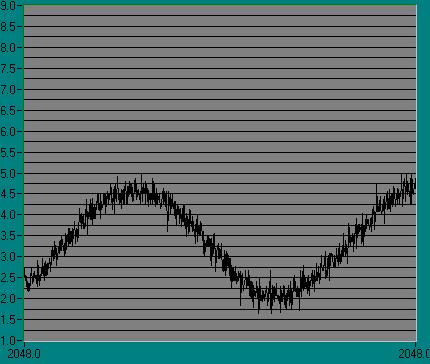
19) Diagram 19: AM time domain signal:

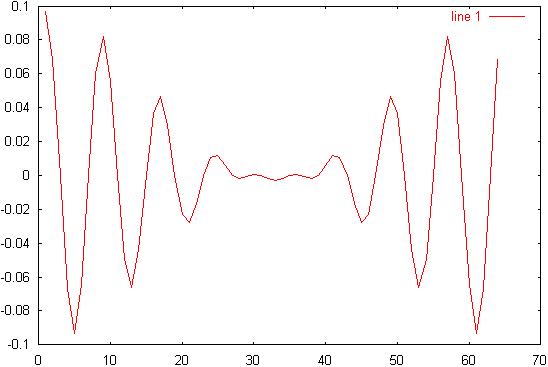
20) Diagram 20: AM signal spectrum:

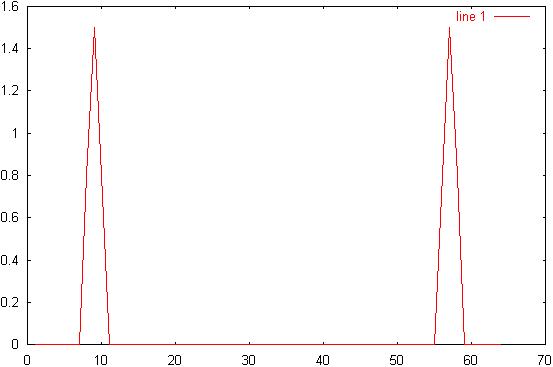
21) Diagram 21: Realized AM signal:

Answers to Lab Questions

1) Q: Given a 1024 sample spectrum, X, where X(24) = 100 and X(108) = 200, where would the complimentary peaks be in the array?

A: X(1001)=100; X(917)=200;

2) Q: What would the time-domain signal be for the spectrum in Q1?

A: x=102*cos(2*pi*23*n/1024) + 204*cos(2*pi*107*n/1024); n=0:1024;

3) Q: Implement a frequency-domain low-pass filter with a cutoff frequency of 6.4KHz where the sampling rate is 25.6KHz, include the capture and reproduction.

A: 1) x=ad(100);

2) X=fft(X);

3) H=ones(1,100);

4) H(26:75)=zeros(1,50);

5) Y=H.*X;

6) y=real(ifft(Y));

7) da(y);

Conclusions

This lab has demonstrated the ability of the Fast Fourrier Transform to transform a signal from the time-domain to the frequency domain. Also, this lab has demonstrated the ability of the hamming window to reduce spectral leakage. The hamming window did not, however, totally eliminate spectral leakage. Also, the AM spectrum looks to be in error. I believe the reason that the AM spectrum looks incorrect is that the amplitude of m, which was arbitrarily set at .8, happened to be in the slope of the carrier, and therefore, the point did not show. For review of signal spectrum generation, please see the log portion of the attachments.

Attachments

Original lab handout
Original lab data
Calculations
Octave® log

GNU Octave, version 2.1.31 (i586-pc-cygwin).

This is free software with ABSOLUTELY NO WARRANTY.

For details, type `warranty'.

*** This is a development version of Octave. Development releases

*** are provided for people who want to help test, debug, and improve

*** Octave.

***

*** If you want a stable, well-tested version of Octave, you should be

*** using one of the stable releases (when this development release

*** was made, the latest stable version was 2.0.16).

octave:1> n=0:15;

octave:2> x = cos(2*pi*n/8);

octave:3> x = cos(2*pi*n/4);

octave:4> plot (x)

octave:5> X =fft(x);

octave:6> plot(abs(X));

octave:7> x = cos(2*pi*n/8);

octave:8> plot (x)

octave:9> X =fft(x);

octave:10> plot(abs(X));

octave:11> x = cos(2*pi*n/16);

octave:12> plot (x)

octave:13> X =fft(x);

octave:14> plot(abs(X));

octave:15> x = cos(2*pi*n/2);

octave:16> plot (x)

octave:17> X =fft(x);

octave:18> plot(abs(X));

octave:19> x = cos(2.1*pi*n/4);

octave:20> plot (x)

octave:21> X =fft(x);

octave:22> plot(abs(X));

octave:23> x2=x.*hamming(16)';

octave:24> plot(x2)

octave:25> X2 =fft(x2);

octave:26> plot(abs(X2));

octave:27> fir(1)

1 coefficients

Max = 1.000000

Scale factor = 4.000000

Scale shift = 2

float hex

b[0] = 1.0000 4000

octave:28> x=ad(100);

k = 100

octave:29> plot(x)

octave:30> x=fft(X);

error: `X' undefined near line 30 column 7

error: evaluating argument list element number 1

error: evaluating index expression near line 30, column 3

error: evaluating assignment expression near line 30, column 2

octave:30> X=fft(x);

octave:31> plot(abs(X))

octave:32> X=zeros(1,16);

octave:33> X(2)=1;

octave:34> X(16)=1;

octave:35> x=real(ifft(X));

octave:36> plot(abs(X))

octave:37> plot(x)

octave:38> x=8192.*x;

octave:39> da(x)

k = 16

x[0] = 1024.000000

x[1] = 946.052612

x[2] = 724.077332

x[3] = 391.867828

x[4] = 0.000000

x[5] = -391.867828

x[6] = -724.077332

x[7] = -946.052612

x[8] = -1024.000000

x[9] = -946.052612

x[10] = -724.077332

x[11] = -391.867828

x[12] = 0.000000

x[13] = 391.867828

x[14] = 724.077332

x[15] = 946.052612

xint[0] = 1024

xint[1] = 946

xint[2] = 724

xint[3] = 391

xint[4] = 0

xint[5] = -391

xint[6] = -724

xint[7] = -946

xint[8] = -1024

xint[9] = -946

xint[10] = -724

xint[11] = -391

xint[12] = 0

xint[13] = 391

xint[14] = 724

xint[15] = 946

octave:40> AM=zeros(1,64);

octave:41> AM(9)=1.5;

octave:42> AM(57)=1.5;

octave:43> AM(8)=.8;

octave:44> AM(10)=.8;

octave:45> AM(56)=.8;

octave:46> AM(58)=.8;

octave:47> am=real(ifft(AM));

octave:48> plot(am)

octave:49> plot(AM)

octave:50> da(am)

k = 64

x[0] = 0.096875

x[1] = 0.068331

x[2] = 0.000000

x[3] = -0.066979

x[4] = -0.093069

x[5] = -0.064326

x[6] = 0.000000

x[7] = 0.060476

x[8] = 0.082230

x[9] = 0.055575

x[10] = 0.000000

x[11] = -0.049812

x[12] = -0.066009

x[13] = -0.043409

x[14] = 0.000000

x[15] = 0.036611

x[16] = 0.046875

x[17] = 0.029680

x[18] = 0.000000

x[19] = -0.022883

x[20] = -0.027741

x[21] = -0.016479

x[22] = 0.000000

x[23] = 0.010716

x[24] = 0.011520

x[25] = 0.005816

x[26] = 0.000000

x[27] = -0.001965

x[28] = -0.000681

x[29] = 0.000687

x[30] = 0.000000

x[31] = -0.002039

x[32] = -0.003125

x[33] = -0.002039

x[34] = 0.000000

x[35] = 0.000687

x[36] = -0.000681

x[37] = -0.001965

x[38] = 0.000000

x[39] = 0.005816

x[40] = 0.011520

x[41] = 0.010716

x[42] = 0.000000

x[43] = -0.016479

x[44] = -0.027741

x[45] = -0.022883

x[46] = 0.000000

x[47] = 0.029680

x[48] = 0.046875

x[49] = 0.036611

x[50] = 0.000000

x[51] = -0.043409

x[52] = -0.066009

x[53] = -0.049812

x[54] = 0.000000

x[55] = 0.055575

x[56] = 0.082230

x[57] = 0.060476

x[58] = 0.000000

x[59] = -0.064326

x[60] = -0.093069

x[61] = -0.066979

x[62] = 0.000000

x[63] = 0.068331

xint[0] = 0

xint[1] = 0

xint[2] = 0

xint[3] = 0

xint[4] = 0

xint[5] = 0

xint[6] = 0

xint[7] = 0

xint[8] = 0

xint[9] = 0

xint[10] = 0

xint[11] = 0

xint[12] = 0

xint[13] = 0

xint[14] = 0

xint[15] = 0

xint[16] = 0

xint[17] = 0

xint[18] = 0

xint[19] = 0

xint[20] = 0

xint[21] = 0

xint[22] = 0

xint[23] = 0

xint[24] = 0

xint[25] = 0

xint[26] = 0

xint[27] = 0

xint[28] = 0

xint[29] = 0

xint[30] = 0

xint[31] = 0

xint[32] = 0

xint[33] = 0

xint[34] = 0

xint[35] = 0

xint[36] = 0

xint[37] = 0

xint[38] = 0

xint[39] = 0

xint[40] = 0

xint[41] = 0

xint[42] = 0

xint[43] = 0

xint[44] = 0

xint[45] = 0

xint[46] = 0

xint[47] = 0

xint[48] = 0

xint[49] = 0

xint[50] = 0

xint[51] = 0

xint[52] = 0

xint[53] = 0

xint[54] = 0

xint[55] = 0

xint[56] = 0

xint[57] = 0

xint[58] = 0

xint[59] = 0

xint[60] = 0

xint[61] = 0

xint[62] = 0

xint[63] = 0

octave:51> am=8192.*am;

octave:52> da(am)

k = 64

x[0] = 793.599976

x[1] = 559.765259

x[2] = 0.000000

x[3] = -548.688538

x[4] = -762.421082

x[5] = -526.960693

x[6] = 0.000000

x[7] = 495.416748

x[8] = 673.630920

x[9] = 455.268921

x[10] = 0.000000

x[11] = -408.060089

x[12] = -540.747131

x[13] = -355.604431

x[14] = 0.000000

x[15] = 299.917786

x[16] = 384.000000

x[17] = 243.140213

x[18] = 0.000000

x[19] = -187.453583

x[20] = -227.252869

x[21] = -134.997925

x[22] = 0.000000

x[23] = 87.789085

x[24] = 94.369064

x[25] = 47.641262

x[26] = 0.000000

x[27] = -16.097321

x[28] = -5.578943

x[29] = 5.630523

x[30] = 0.000000

x[31] = -16.707281

x[32] = -25.600000

x[33] = -16.707281

x[34] = 0.000000

x[35] = 5.630523

x[36] = -5.578943

x[37] = -16.097321

x[38] = 0.000000

x[39] = 47.641262

x[40] = 94.369064

x[41] = 87.789085

x[42] = 0.000000

x[43] = -134.997925

x[44] = -227.252869

x[45] = -187.453583

x[46] = 0.000000

x[47] = 243.140213

x[48] = 384.000000

x[49] = 299.917786

x[50] = 0.000000

x[51] = -355.604431

x[52] = -540.747131

x[53] = -408.060089

x[54] = 0.000000

x[55] = 455.268921

x[56] = 673.630920

x[57] = 495.416748

x[58] = 0.000000

x[59] = -526.960693

x[60] = -762.421082

x[61] = -548.688538

x[62] = 0.000000

x[63] = 559.765259

xint[0] = 793

xint[1] = 559

xint[2] = 0

xint[3] = -548

xint[4] = -762

xint[5] = -526

xint[6] = 0

xint[7] = 495

xint[8] = 673

xint[9] = 455

xint[10] = 0

xint[11] = -408

xint[12] = -540

xint[13] = -355

xint[14] = 0

xint[15] = 299

xint[16] = 384

xint[17] = 243

xint[18] = 0

xint[19] = -187

xint[20] = -227

xint[21] = -134

xint[22] = 0

xint[23] = 87

xint[24] = 94

xint[25] = 47

xint[26] = 0

xint[27] = -16

xint[28] = -5

xint[29] = 5

xint[30] = 0

xint[31] = -16

xint[32] = -25

xint[33] = -16

xint[34] = 0

xint[35] = 5

xint[36] = -5

xint[37] = -16

xint[38] = 0

xint[39] = 47

xint[40] = 94

xint[41] = 87

xint[42] = 0

xint[43] = -134

xint[44] = -227

xint[45] = -187

xint[46] = 0

xint[47] = 243

xint[48] = 384

xint[49] = 299

xint[50] = 0

xint[51] = -355

xint[52] = -540

xint[53] = -408

xint[54] = 0

xint[55] = 455

xint[56] = 673

xint[57] = 495

xint[58] = 0

xint[59] = -526

xint[60] = -762

xint[61] = -548

xint[62] = 0

xint[63] = 559

octave:53>