EE - 453 / E01 Fall 2003

Control I

Professor: Thomas

Submitted By:

Andrew Buettner

Lab #2: Car Suspension System

Tuesday, December 09, 2003

Table Of Contents

1) Cover Page 1

2) Table of Contents 2

3) Objective 3

4) Components Used 3

5) Procedures 3

6) Lab Data / Results 3



1) Table 1 3

2) Diagram 1 4

3) Table 2 4

4) Diagram 2 5

5) Table 3 5

6) Diagram 3 5

7) Diagram 4 6

8) Diagram 5 6

9) Diagram 6 7

10) Diagram 7 7

11) Diagram 8 8

7) Conclusions 8

8) Attachments 8

Objective

The objective of this lab is to model the suspension system of a car over an arbitrary terrain using MatLab® or similar software. The various coefficients for the system will be given. The system will be modeled and a transfer function will be obtained both directly and by using Mason's Gain Rule. A unit step function will be applied to the system modeled in MatLab® and the resulting displacement of the wheel and vehicle will be observed.

Components Used

1) PC with MatLab®, Octave®, SciLab® or equivalent.

Procedure

1) Given values, model a vehicle suspension system in the Laplace domain.

2) Obtain the transfer function to describe the displacement of the wheel and the vehicle body.

3) Obtain the signal flow graph of the system.

4) Using the Signal Flow Graph and Mason's gain rule, obtain the transfer function of the system.

5) Using MatLab®, or equivalent, graph the step response of the system.

6) Repeat step 4 using a step amplitude of .0112 and compare the results.

Lab Data / Results

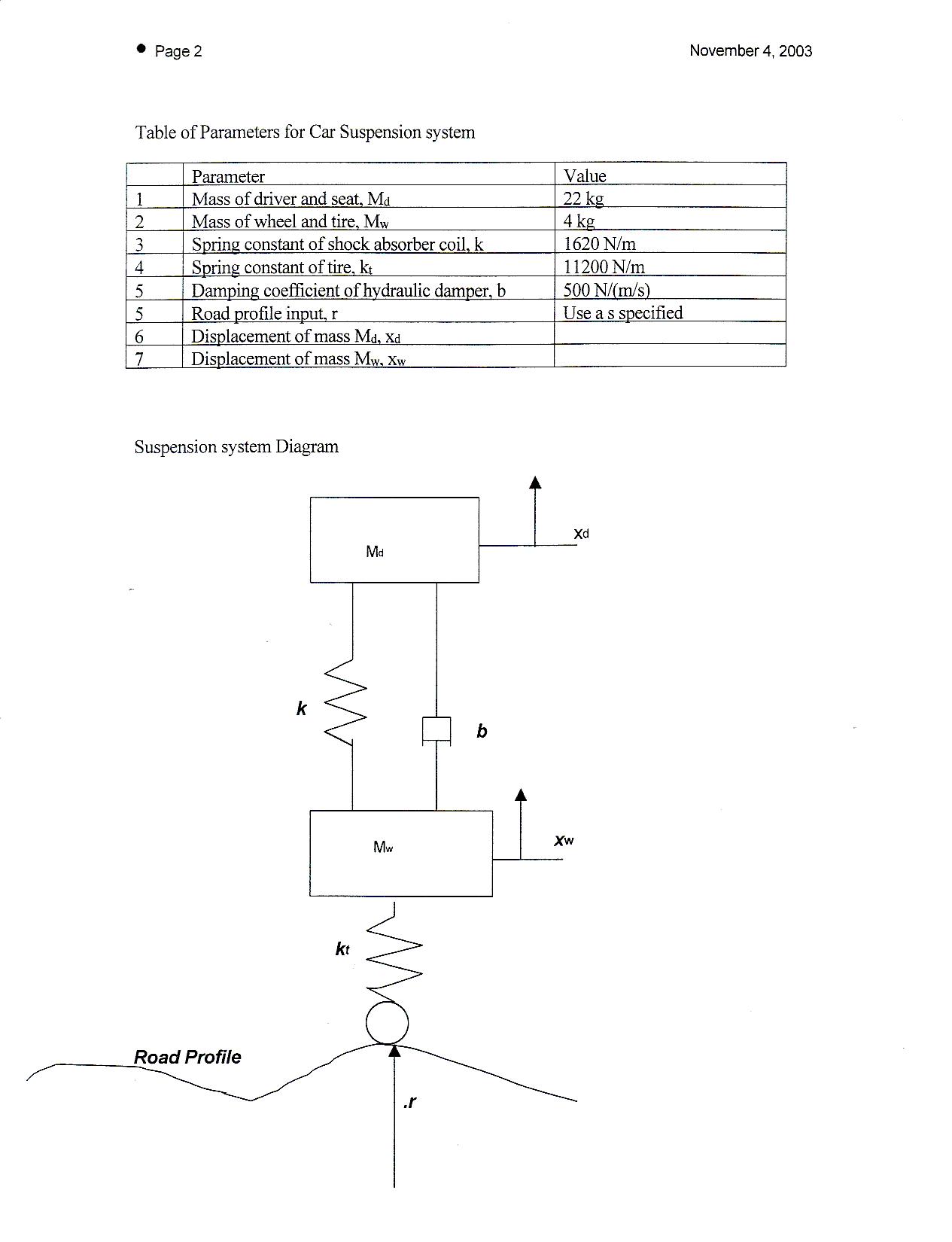
1) Table 1: Car Suspension System Data

Parameter	Value
Vehicle Mass (Md)	22Kg
Mass of Wheel (Mw)	4Kg
Spring Constant of Shock Absorber (k)	1620N/m
Spring Constant of Tire (kt)	11200N/m
Damping Coefficient of Hydraulic Damper (b)	500Ns/m

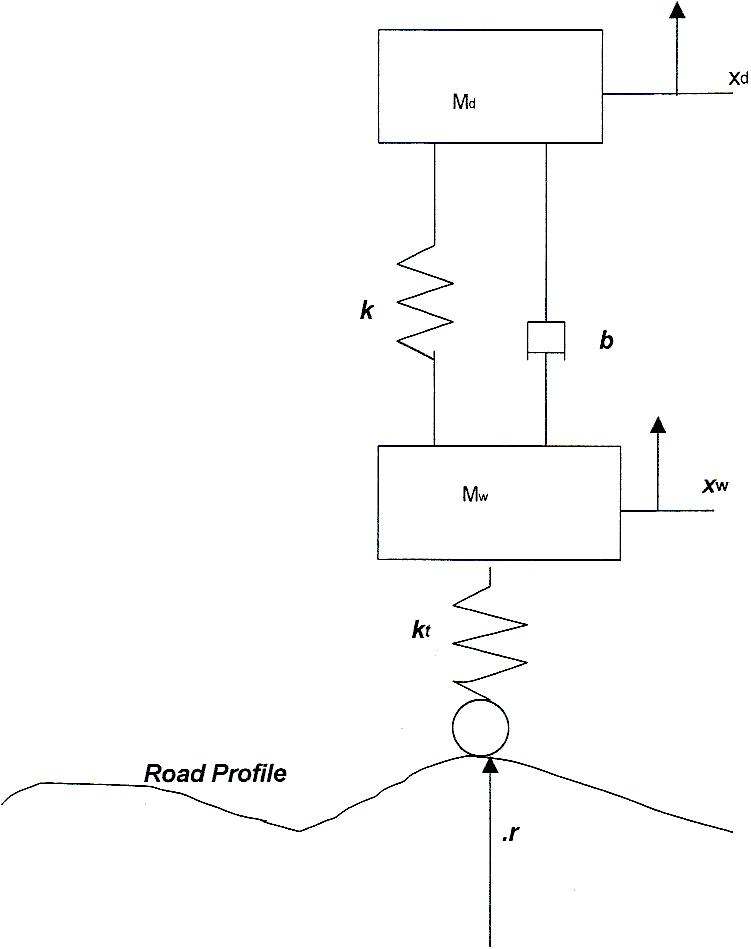
2) Diagram 1: System




3) Table 2: Transfer Functions

Transfer:		Function:
G(s)	=	Xd(s)/R(s)
Xd(s)/R(s)	=	kt*(b*s + k)/((k + kt + b*s + Mw*s2)*(Md*s2 + b*s + k) – (b*s + k)2
Xw(s)/Xd(s)	=	(Md*s2 + b*s + k)/(b*s + k)

4) Diagram 2: Signal Flow Graph




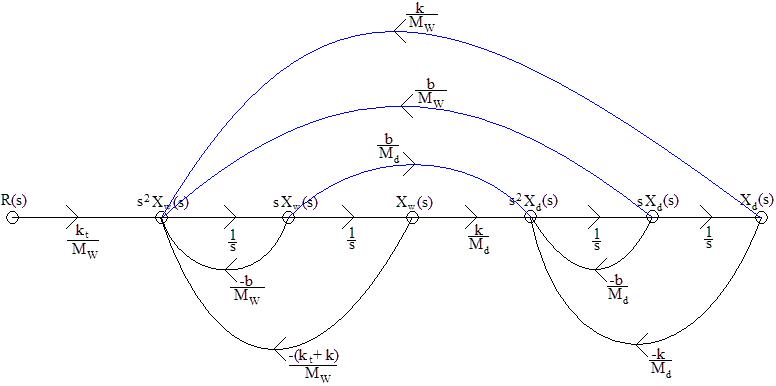
5) Table 3: Transfer Function from Signal Flow Graph

Transfer:		Function:
G(s)	=	kt*(k + b*s)/((Mw*s2 + b*s + kt + k)*(Md*s2 + b*s + k) – (b*s + k)2

6) Diagram 3: System Response to a Unit Step Input


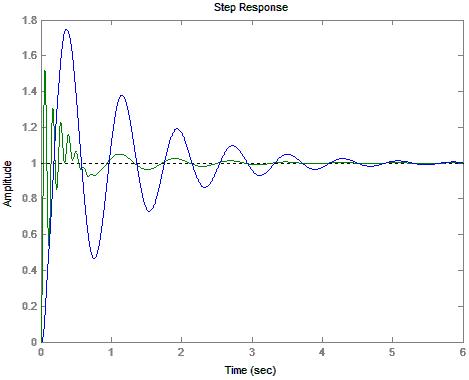
7) Diagram 4: Wheel Response to a Unit Step Input




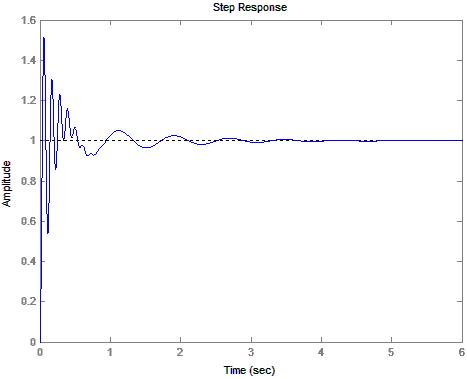
8) Diagram 5: Driver Response to a unit Step Input


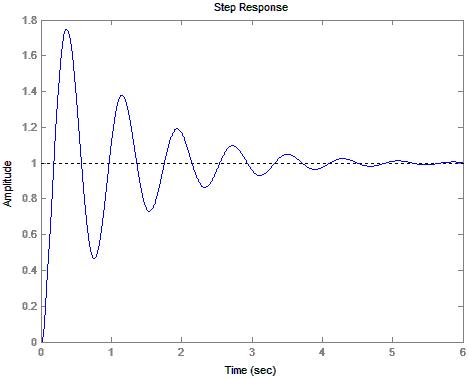
9) Diagram 6: System Response to a Unit Step Input of Amplitude .0112




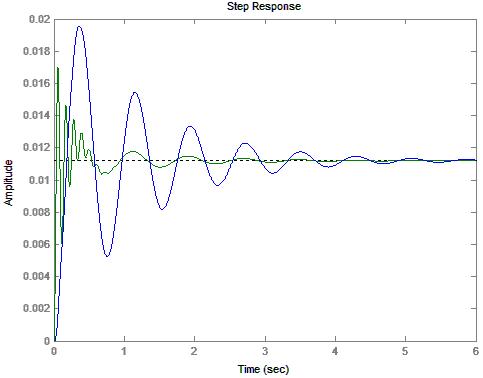
10) Diagram 7: Wheel Response to a Unit Step Input of Amplitude .0112


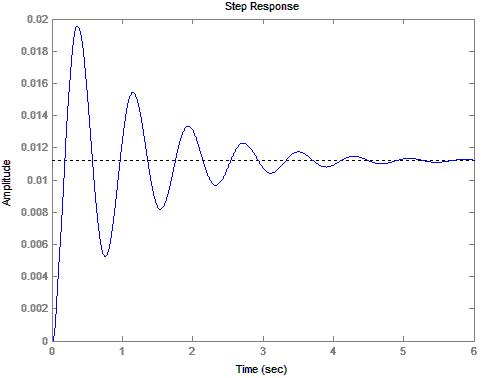
11) Diagram 8: Driver Response to a Unit Step Input of Amplitude .0112




Conclusions

This lab has demonstrated that a system may be modeled both through Mason's gain rule as well as through the use of force diagrams. The transfer functions, after a significant amount of work, can be show to be equivalent. (Please refer to Attachments 3.1). Additionally, programs like MatLab® can be used to simulate the system. The effect of applying a .0112 unit step in step 6 caused a scaling factor to be applied to the transfer function. This in turn, scaled the responses. Although otherwise identical, the response was significantly smaller. This corresponds to things observed today. If you hit a large curb you're in for much more of a rough ride than if you roll over a small rock.

Attachments

1. Original lab handout

2. Original lab data

3. Calculations

4. MatLab® log

>> Lab2(1)

>> Lab2(.0112)

>>