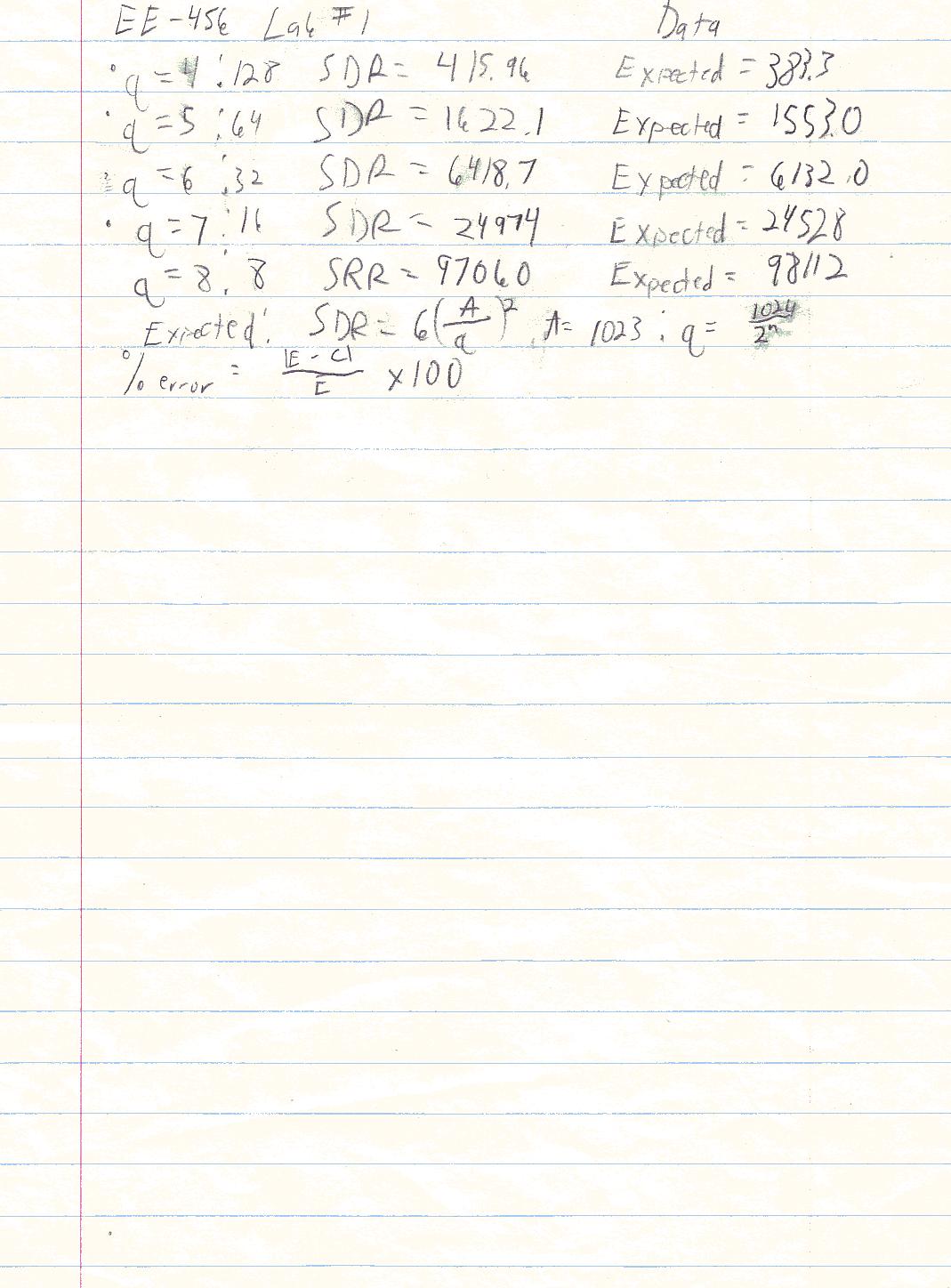Objective
The objective of this lab is to quantize sinewaves and compute the signal-to-noise ratio. The results will be compared to a predicted value that will be computed through a given formula.
Components Used
1) Computer with Octave installed
Procedures
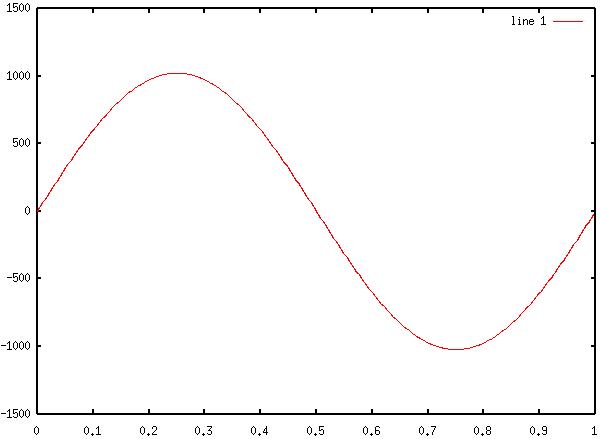
1) Generate a 512 sample sinewave with f=1Hz and an amplitude of 1023
2) Plot the signal
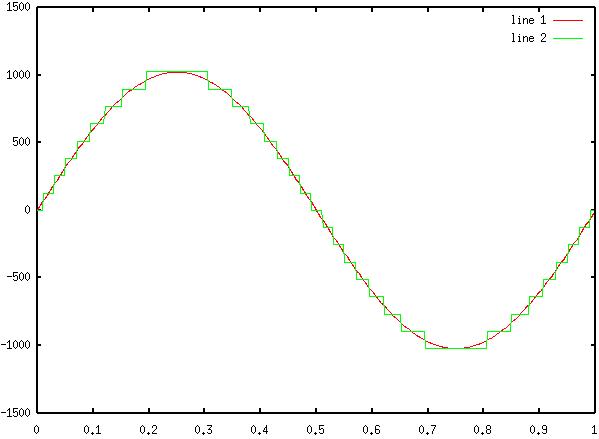
3) Quantize the signal using the command "xq = 128*round(x./128);"
4) Plot both functions
5) Create function "d" that is the difference between "x" and "xq"
6) Plot all three functions.
7) Calculate the variance using "vx=(x*x')./511"
8) Calculate the variance of d using a similar method
9) Calculate the distortion ratio using SDR=vx/vd
10) Compare to an expected distortion ratio 6*(A/q)^2
11 Repeat steps 3 - 9 for quantization of 5, 6, 7, and 8 bits, only plot the culmination of all three functions.
Lab
Data / Results
1) Table 1: Signal to Distortion Results
|
Number of Bits |
Quantization Interval |
Observed SDR |
Expected SDR |
% Error |
|---|---|---|---|---|
|
Q = 4 |
128 |
415.96 |
383.3 |
8.52% |
|
Q = 5 |
64 |
1622.1 |
1553.0 |
4.45% |
|
Q = 6 |
32 |
6418.7 |
6132.0 |
4.68% |
|
Q = 7 |
16 |
24974 |
24528 |
1.82% |
|
Q = 8 |
8 |
97060 |
98112 |
1.07% |
2) Diagram 1: Original Sinewave
3) Diagram
2: Original Sinewave and 4 bit Quantized Wave
4) Diagram
3: Original Sinewave, 4 bit Quantized, and Difference
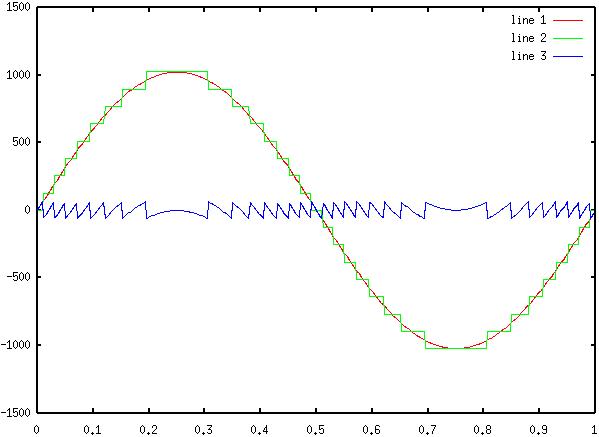
5) Diagram
4: Original Sinewave, 5 bit Quantized, and Difference
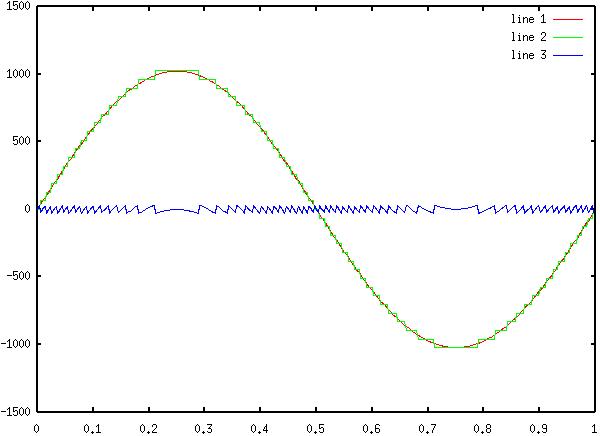
6) Diagram
5: Original Sinewave, 6 bit Quantized, and Difference
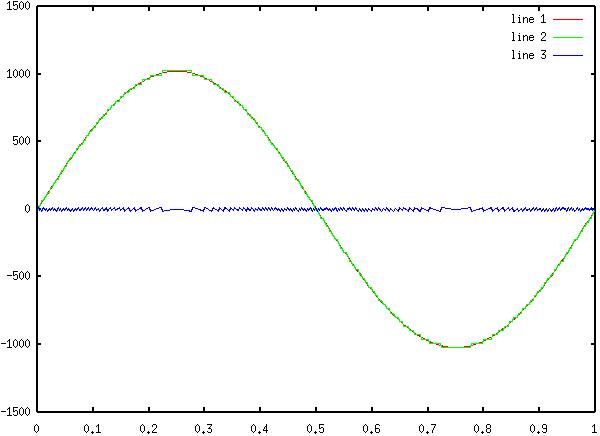
7) Diagram
6: Original Sinewave, 7 bit Quantized, and Difference
8) Diagram
7: Original Sinewave, 8 bit Quantized, and Difference
Answer to Lab Questions
1) Q: Derive the formula SDR=6*(A/q)2
A: See Attachments::Calculations
2) Q: Given a quantized array, derive a set of MatLab® commands that will discover the number of bits used to encode the aray.
A: Assuming the signal is sinusoidal and has an absolute average of 0
1) vxq=(xq*xq')./N; (N is the number of samples in xq)
2) int=max(xq) - min(xq);
3) q=round(log(int)/log(2))
3) Q: What formula would be used to describe the signal - to - distortion ratio if truncation were used, instead of rounding.
A: SDRT Z 3*(A/q)2
Conclusions
This lab has demonstrated the effect of voltage quantizing on a signal. It has illustrated two different methods of computing the signal - to distortion ratio. Both methods yield fairly accurate results (<10% error). It is interesting that the higher the number of bits used in quantization, the lower the error was in predicting the SDR. This gives a practical formula (S 1% for eight or more bits) for quantization. However, I believe that the ratio of deviations is a much more accurate formula, and actually yielded the correct results, as opposed to the formula. It appears that the value 6 needs to be greater for larger quantization interval, and less for smaller intervals.
Attachments
