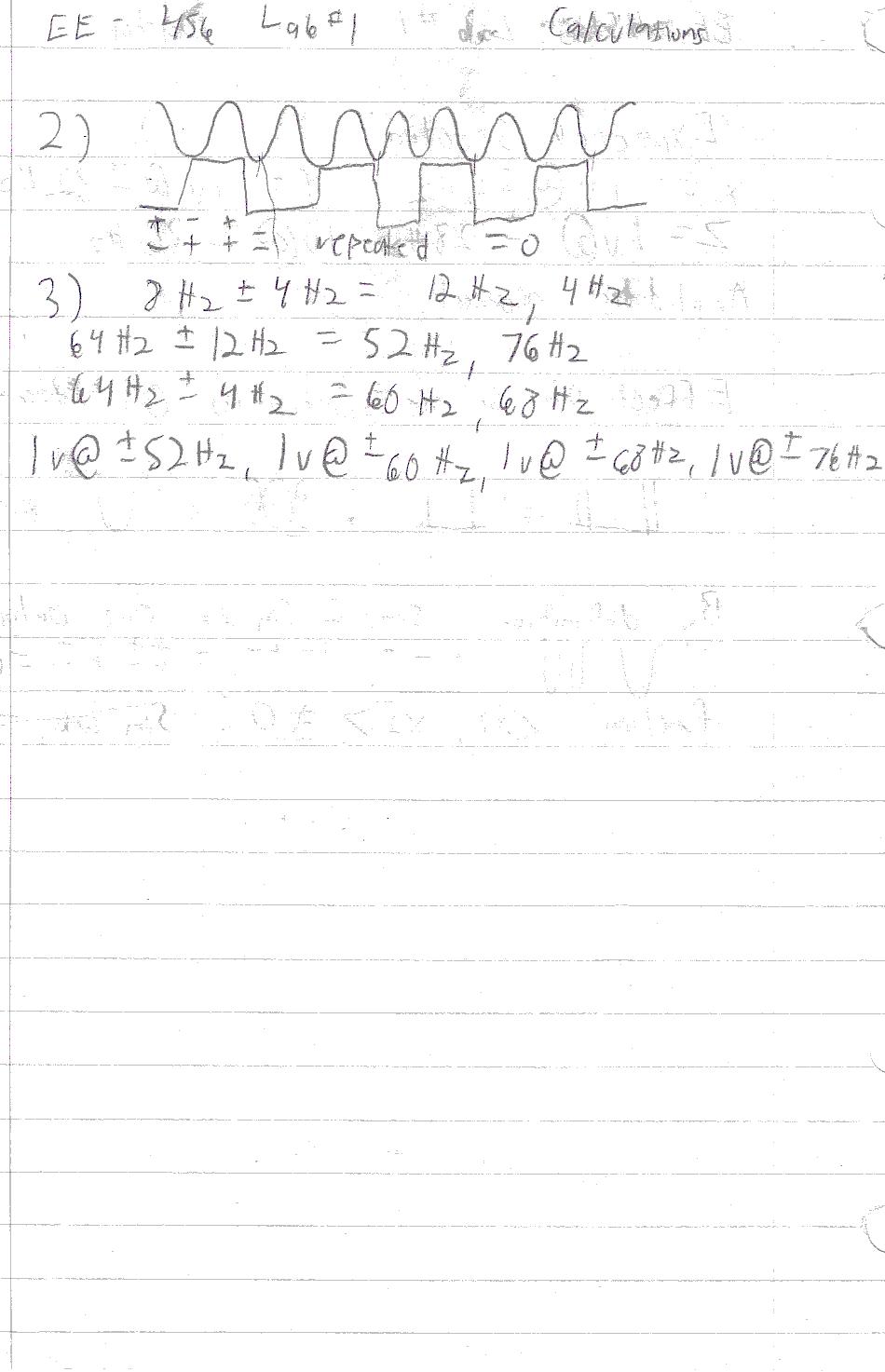EE - 451 / E01 spring 2003

Advanced Communications Theory

Professor: Conner

Submitted By:

Andrew Buettner

Lab #1: Introduction to MATLAB, Signals and Spectra

Sunday, March 02, 2003

Table Of Contents

1) Cover Page 1

2) Table of Contents 2

3) Objective 3

4) Components Used 3

5) Procedures 3

6) Lab Data / Results 4



1) Diagram 1 4

2) Diagram 2 4

3) Diagram 3 5

4) Diagram 4 5

5) Diagram 5 6

6) Diagram 6 6

7) Diagram 7 7

8) Diagram 8 7

9) Diagram 9 8

10) Diagram 10 8

11) Diagram 11 9

12) Diagram 12 9

13) Diagram 13 10

14) Diagram 14 10

7 Answers to Lab Questions 11

7) Conclusions 11

8) Attachments 11

• Objective

  The objective of this lab is to gain a fundamental understanding of the MatLab^[TM] application. This will be accomplished by applying various simulation techniques. Simulation is necessary as the circuits themselves are too complicated to be realized reasonably.

• Components Used

  1) PC with MatLab^[TM], octave, or SciLab installed.

• Procedures

  1) Using MatLab, or another program simulate a 4Hz cosine wave by using the following commands:

  a) n=0:255;

  b) t=n/256;

  c) f=4;

  d) omega=2*pi*f;

  e) x=cos(omega*t);

  f) plot(t,x);

  2) Create a second signal in the same manner with f=32Hz, and plot both using "plot(t,x,t,y)"

  3) Create a new function, z(t) = x(t)*y(t) by using "z = x.*y;"

  4) Plot all three functions

  5) Using the fft function, plot the spectra using X(1:256) to display the spectra of x(t), y(t), and z(t).

  6) Justify that the spectra are correct.

  7) Re-compute Z = fft(z)

  8) Set the 37^th and 221^st sample of the Z array to zero.

  9) Explain what effect this has on the signal.

  10) Using the command "z=real(ifft(Z));" plot the filtered time domain function.

  11) Justify the waveform.

  12) Find the dot product between x(t) and y(t) using "xy = x*y'"

  13) Justify the value produced, and determine if the functions are orthogonal.

  14) Find two functions that are orthogonal to x(t) and have the same frequency as x(t).

  15) Verify, using the program, that the functions are, in fact, orthogonal to x(t).

• Lab Data / Results

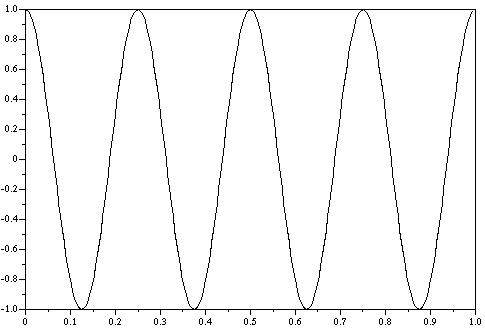
  1) Diagram 1: SciLab output for 4Hz sinewave

  
  

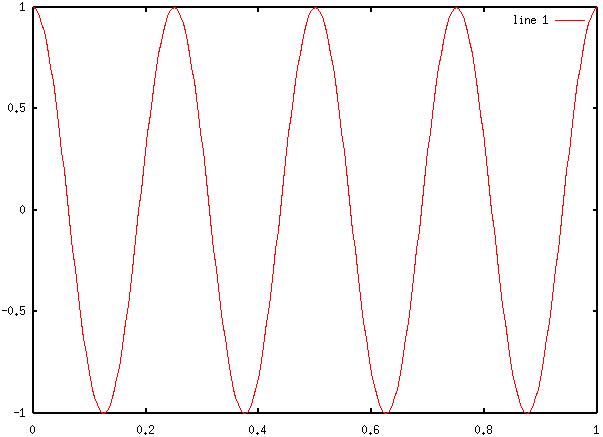
  2) Diagram 2: Octave output for 4Hz sinewave

  
  

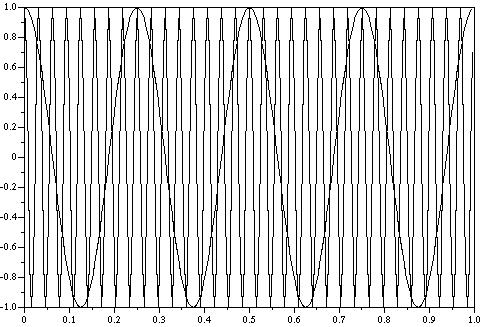
  3) Diagram 3: SciLab output for combination of 32Hz and 4Hz sinewaves.

  
  

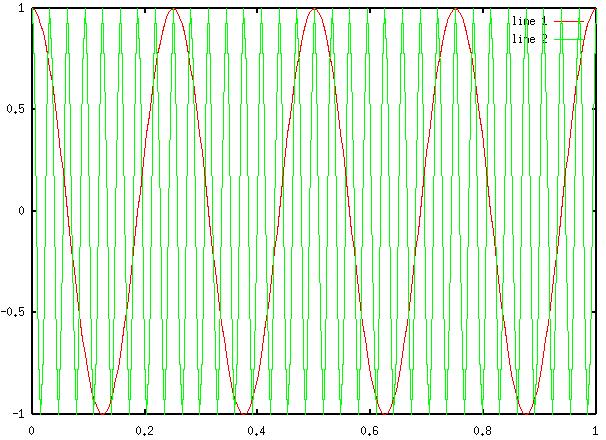
  4) Diagram 4: Octave output for combination of 32Hz and 4Hz sinewaves.

  
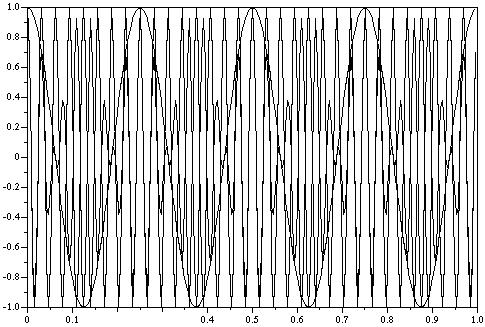
  5) Diagram 5: SciLab output for 32Hz sinewave, 4Hz sinewave, and the resulting waveform of the two multiplied together.

  
  

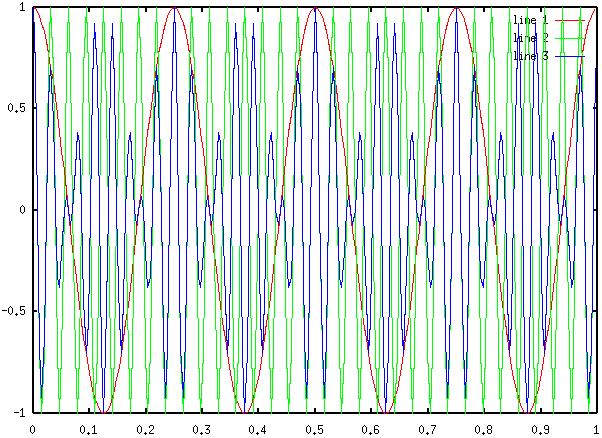
  6) Diagram 6: Octave output for 32Hz sinewave, 4Hz sinewave, and the resulting waveform of the two multiplied together.

  
  

  7) Diagram 7: SciLab output of fft(y(t))

  
  

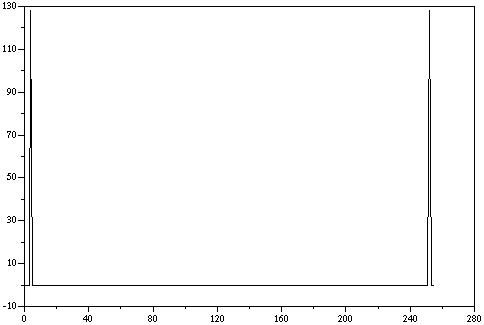
  8) Diagram 8: Octave output of fft(y(t))

  
  

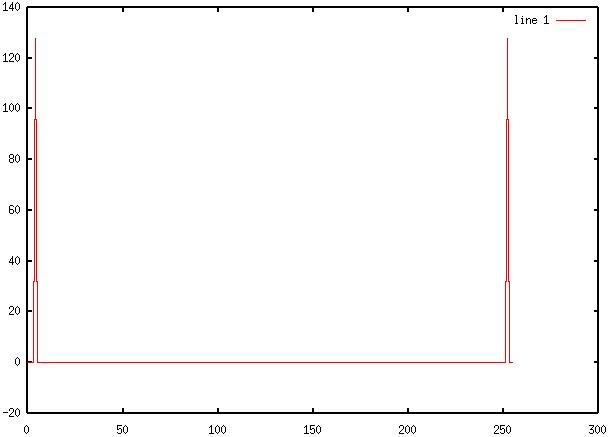
  9) Diagram 9: SciLab output of fft(y(t))

  
  

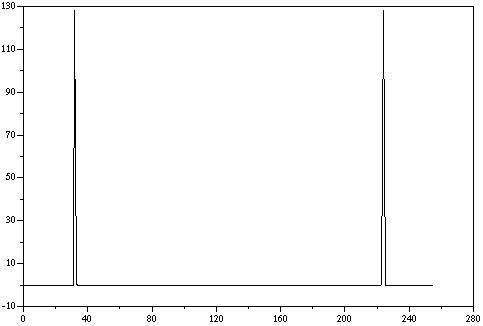
  10) Diagram 10: Octave output of fft(y(t))

  
  

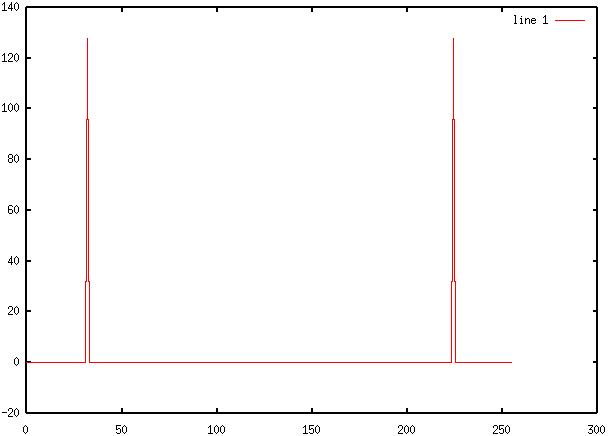
  11) Diagram 11: SciLab output of fft(z(t))

  
  

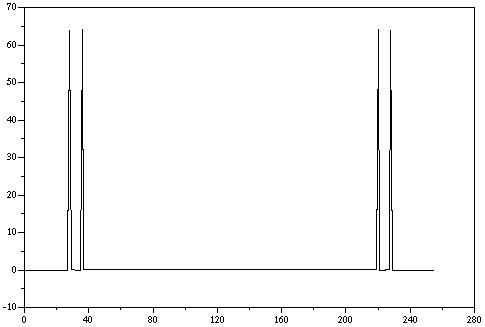
  12) Diagram 12: Octave output of fft(z(t))

  
  

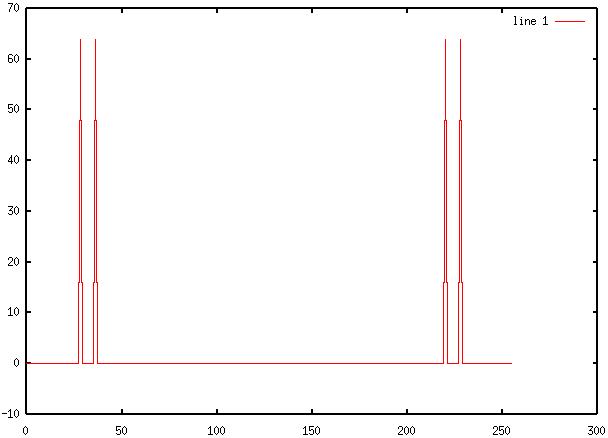
  13) Diagram 13: SciLab filtered time-domain signal

  
  

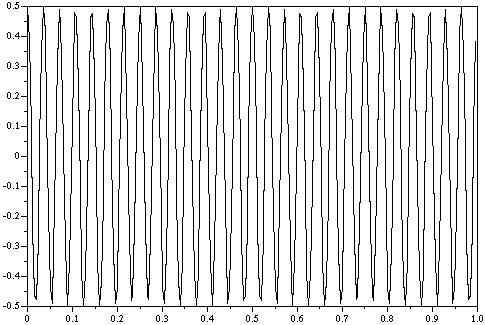
  14) Diagram 14: Octave filtered time-domain signal

  
  

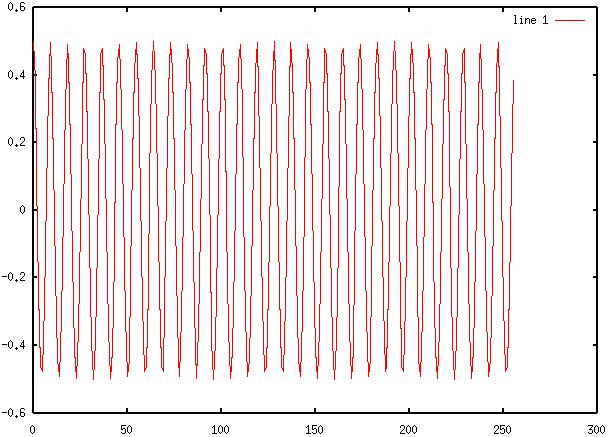
• Answers to Lab Questions

  1) Q: Find the exponential Fourier series of x(t), y(t), and z(t), how do they compare to X, Y, and Z?

  A: x(t) = 1v @ +/- 4Hz - The spectra is correct except for the amplitude; y(t) = 1v @ +/- 32Hz - The spectra is correct except for the amplitude; z(t) = 1v @ +/- 28Hz, 1v @ +/- 36Hz - The spectra is correct except for the amplitude.

  2) Q: Given an 4Hz squarewave and a 8Hz sinewave, how could MatLab be used to prove that they are orthogonal, prove it analytically.

  A: Simulate the waves using a -1^n exponential series for the squarewave, and the cosine directly for the sinewave. Use the operator "xy=x*y'"

  3) Q: Given sinewaves of 4Hz, 8Hz, and 64Hz, find the spectrum of the product of the waves.

  A: 1v @ +/- 52Hz, 1v @ +/-60Hz, 1v @ +/-68Hz, 1v @ +/- 76Hz

• Conclusions

  This lab has demonstrated the basics of the MatLab command set. I do not have the ability to run MatLab on any computer, so instead, I chose to run a combination of SciLab and GNU Octave. I found that the Octave had more inherent variables (pi, etc) and was slightly more accurate, and had syntax closer to MatLab, but SciLab had a lot more functions, including those that interfaced with the system DSP. For the exact command structure, please refer to the attachments.

• Attachments

1. Original lab handout

2. Original lab data

3. Calculations

4. Octave log

5. SciLab log

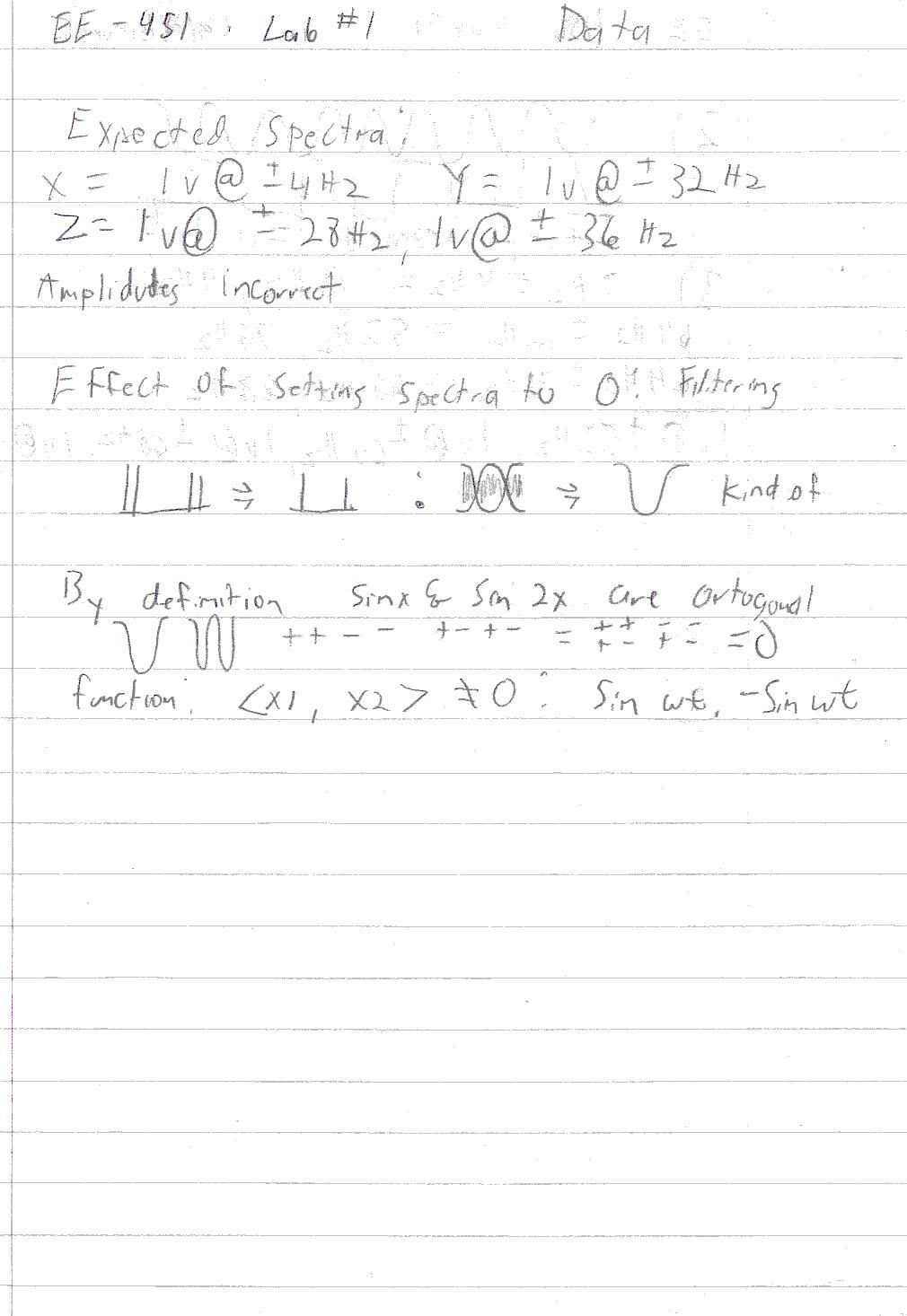
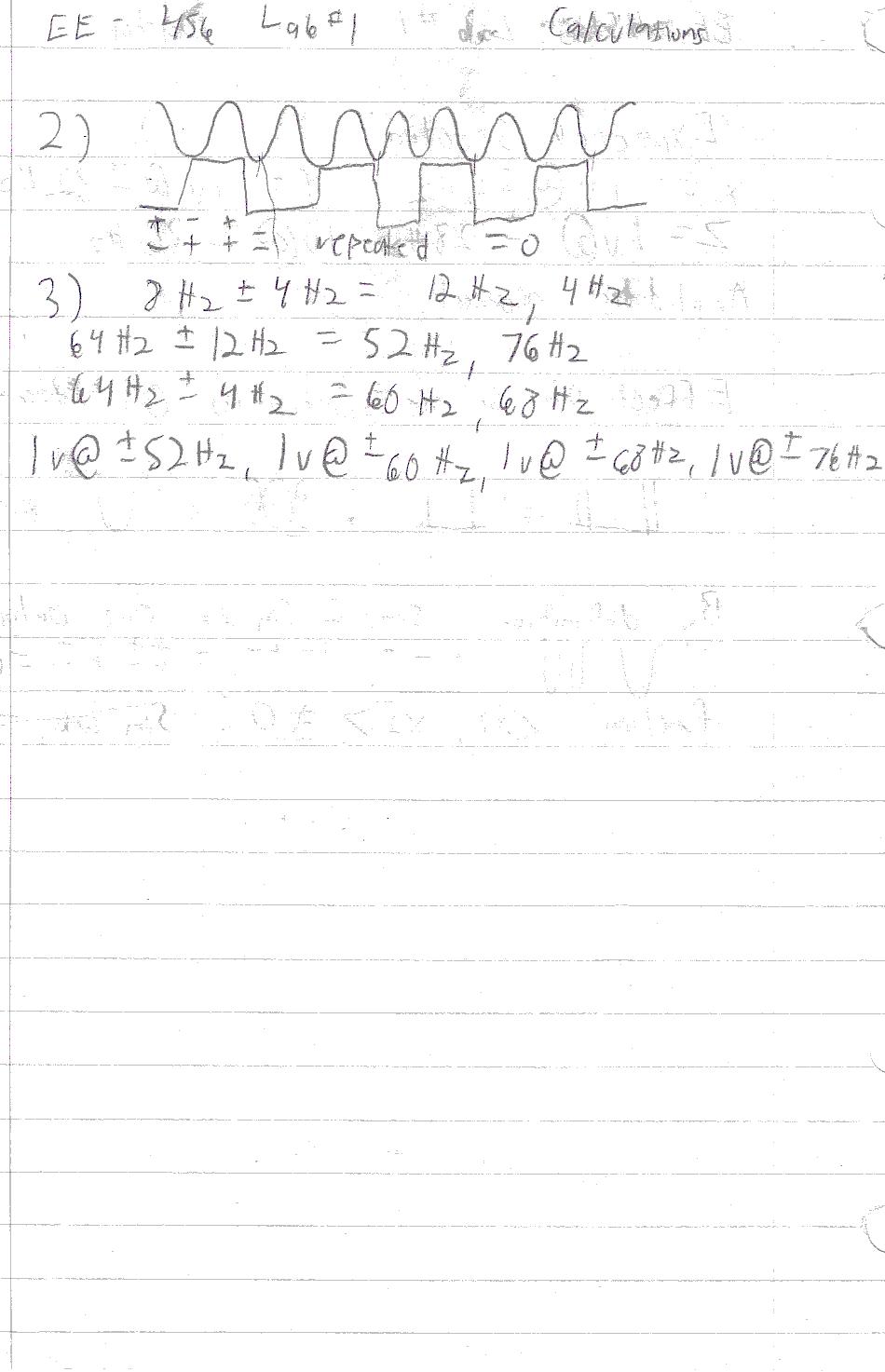
GNU Octave, version 2.0.17 (i686-pc-linux-gnu).

Copyright (C) 1996, 1997, 1998, 1999, 2000, 2001, 2002 John W. Eaton.

This is free software with ABSOLUTELY NO WARRANTY.

For details, type `warranty'.

octave:1> pi

pi = 3.1416

octave:2> n=0:255;

octave:3> t=n/256;

octave:4> f=4;

octave:5>

octave:5> omega=2*pi*f;

octave:6> x=cos(omega*t);

octave:7> plot(t,x);

octave:8>

octave:8>

octave:8> f2=32;

octave:9> omega2=2*pi*f2;

octave:10> y=cos(omega2*t);

octave:11> plot(t,x,t,y);

octave:12> z=x.*y;

octave:13> plot(t,x,t,y,t,z)

octave:14> X(1:64)=fft(z);

error: A(I) = X: X must be a scalar or a vector with same length as I

error: evaluating assignment expression near line 14, column 8

octave:14> X(1:256)=fft(z);

octave:15> plot(X)

octave:16> plot(t,X)

octave:17> plot(n,X)

octave:18> X(1:256)=fft(x);

octave:19> plot(n,X)

octave:20> X(1:256)=fft(y);

octave:21> plot(n,X)

octave:22> X(1:256)=fft(y)

octave:23> n2=0:64;

octave:24> plot(n2,X);

error: __plt2vv__: vector lengths must match

error: evaluating index expression near line 52, column 5

error: evaluating if command near line 51, column 3

error: called from `__plt2vv__' in file `/usr/local/share/octave/2.0.17/m/plot/__plt2vv__.m'

error: called from `__plt2__' in file `/usr/local/share/octave/2.0.17/m/plot/__plt2__.m'

error: called from `__plt__' in file `/usr/local/share/octave/2.0.17/m/plot/__plt__.m'

error: called from `plot' in file `/usr/local/share/octave/2.0.17/m/plot/plot.m'octave:24> X(1:256)=fft(x);

octave:25> plot(n,X);

octave:26> X(1:256)=fft(y);

octave:27> plot(n,X);

octave:28> X(1:256)=fft(z);

octave:29> plot(n,X);

octave:30> Z=fft(z);

octave:31> Z(37)

ans = 6.4000e+01 - 3.2880e-13i

octave:32> Z(1:256)=fft(z);

octave:33> Z(37)

ans = 6.4000e+01 - 3.2880e-13i

octave:34> plot(n,Z);

octave:35> Z(1:256)=fft(z)

octave:36> z(37)

ans = 0.92388

octave:37> Z(37)

ans = 6.4000e+01 - 3.2880e-13i

octave:38> Z(37)=0;

octave:39> Z(221)=0;

octave:40> plot(n,Z);

octave:41> z=real(ifft(Z));

octave:42> plot(n,z);

octave:43> xy=x*y;

error: operator *: nonconformant arguments (op1 is 1x256, op2 is 1x256)

error: evaluating assignment expression near line 43, column 3

octave:43> xy=x*y';

octave:44> xy=x*y'

xy = 5.0583e-16

octave:45> x1

error: `x1' undefined near line 45 column 1

error: evaluating expression near line 45, column 1

octave:45> x1=sin(omega*t);

octave:46> plot(t,x1)

octave:47> xy1=x1*x'

xy1 = 5.2718e-15

octave:48> x2=squarewave(t);

error: `squarewave' undefined near line 48 column 4

error: evaluating index expression near line 48, column 4

error: evaluating assignment expression near line 48, column 3

octave:48> x2=-sin(omega*t);

octave:49> plot(t,x2);

octave:50> xy2=x2*x'

xy2 = -5.2718e-15

octave:51>

===========

S c i l a b

===========

scilab-2.6

Copyright (C) 1989-2001 INRIA

Startup execution:

loading initial environment

-->n=0:255;

--> t=n/256;

-->f=4;

-->omega=2*pi*f;

!--error 4

undefined variable : pi

-->pi=3.14156;

-->omega=2*pi*f;

-->x=cos(omega*t);

-->plot(t,x);

-->f2=32;

-->omega2=2*pi*f2;

-->y=cos(omega2*t);

-->plot([t,x][t,y])

!--error 3

waiting for right parenthesis

-->plot2d(t,[x,y])

!--error 999

plot2d: first and second arguments have incompatible dimensions

-->plot2d(t,[x y])

!--error 999

plot2d: first and second arguments have incompatible dimensions

-->n=0:255;

--> t=n/256;

-->plot2d(t,[x y])

!--error 999

plot2d: first and second arguments have incompatible dimensions

-->n=0:255;

--> t=n/256;

-->omega=2*pi*f;

-->pi=3.14156;

-->x=cos(omega*t);

-->f=4;

-->omega2=2*pi*f2;

-->plot2d(t,[x y])

!--error 999

plot2d: first and second arguments have incompatible dimensions

-->plot2d(t, y])

!--error 3

waiting for right parenthesis

-->plot2d(t, y)

-->z=x.*y;

-->plot2d(t, z)

-->X(1:64)=fft(z);

!--error 39

incorrect number of arguments

-->X(1:256)=fft(z);

!--error 39

incorrect number of arguments

-->X(1:255)=fft(z);

!--error 39

incorrect number of arguments

-->X(0:255)=fft(z);

!--error 39

incorrect number of arguments

-->X(0:255)=fft(z)

!--error 39

incorrect number of arguments

-->fft(z)

!--error 39

incorrect number of arguments

-->X(0:255)=fft(z,1);

!--error 21

invalid index

-->X(0:255)=fft(z,-1);

!--error 21

invalid index

-->X(1:256)=fft(z,-1);

-->X(1:256)=fft(z,-1)

X =

column 1 to 3

! - 0.0025193 - 0.0025220 + 9.167E-08i - 0.0025302 + 1.839E-07i !

column 4 to 5

! - 0.0025440 + 2.772E-07i - 0.0025636 + 3.721E-07i !

column 6 to 7

! - 0.0025892 + 4.693E-07i - 0.0026212 + 5.695E-07i !

column 8 to 9

! - 0.0026601 + 6.733E-07i - 0.0027064 + 7.816E-07i !

column 10 to 11

! - 0.0027609 + 8.954E-07i - 0.0028246 + 0.0000010i !

column 12 to 13

[More (y or n ) ?]

-->X(1:256)=fft(z,-1);

-->plot(n,X);

-->X(1:256)=fft(x,-1);

-->plot(n,X);

-->X(1:256)=fft(y,-1);

-->plot(n,X);

-->X(1:256)=fft(z,-1);

-->plot(n,X);

-->Z(1:256)=fft(z,-1);

-->Z(37)=0;

-->Z(221)=0;

-->plot(n,Z);

-->z=real(ifft(Z));

!--error 4

undefined variable : ifft

-->z=realifft(Z,1));

!--error 4

undefined variable : realifft

-->z=real(fft(Z,1));

-->plot(t,z);

-->xy=x*y;

!--error 10

inconsistent multiplication

-->xy=x*y';

-->xy=x*y'

xy =

- 0.0025193

-->x1=sin(omega*t);

-->xy1=x1*x'

xy1 =

0.0001310

-->x2=squarewave(t);

-->plot(t,x2)

-->t

t =

column 1 to 6

-->plot(n,X);

-->Z(1:256)=fft(z,-1);

-->Z(37)=0;

-->Z(221)=0;

-->plot(n,Z);

-->z=real(ifft(Z));

!--error 4

undefined variable : ifft

-->z=realifft(Z,1));

!--error 4

undefined variable : realifft

-->z=real(fft(Z,1));

-->plot(t,z);

-->xy=x*y;

!--error 10

inconsistent multiplication

-->xy=x*y';

-->xy=x*y'

xy =

- 0.0025193

-->x1=sin(omega*t);

-->xy1=x1*x'

xy1 =

0.0001310

-->x2=squarewave(t);

-->plot(t,x2)

-->t

t =

column 1 to 6

! 0. 0.0039062 0.0078125 0.0117188 0.015625 0.0195312 !

column 7 to 11

! 0.0234375 0.0273438 0.03125 0.0351562 0.0390625 !

column 12 to 16

! 0.0429688 0.046875 0.0507812 0.0546875 0.0585938 !

column 17 to 21

! 0.0625 0.0664062 0.0703125 0.0742188 0.078125 !

column 22 to 26

! 0.0820312 0.0859375 0.0898438 0.09375 0.0976562 !

column 27 to 31

[More (y or n ) ?]

-->x2=squarewave(f*t);

-->plot(t,x2)

-->plot2d(t,x2)

-->plot(t,z);

-->plot(t,x2);

-->x2

x2 =

column 1 to 11

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 12 to 22

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 23 to 33

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 34 to 44

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 45 to 55

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 56 to 66

[More (y or n ) ?]

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 67 to 77

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 78 to 88

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 89 to 99

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 100 to 110

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 111 to 121

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 122 to 132

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 133 to 143

[More (y or n ) ?]

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 144 to 154

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 155 to 165

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 166 to 176

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 177 to 187

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 188 to 198

! 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. !

column 199 to 209

! 1. 1. 1. 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. !

[More (y or n ) ?]

column 210 to 220

! - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. !

column 221 to 231

! - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. !

column 232 to 242

! - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. !

column 243 to 253

! - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. - 1. !

column 254 to 256

! - 1. - 1. - 1. !

-->x2=squarewave(omega*t);

-->plot(t,x2);

-->xy2=x2*x'

xy2 =

- 5.97873

-->x2=squarewave(omega*t+(pi/2));

-->xy2=x2*x'

xy2 =

162.84382

-->j=sqrt(-1)

j =

i

-->j=sqrt(-1);

-->e

!--error 4

undefined variable : e

-->x2=exp(j*omega*t);

-->plot(t,x2);

-->x2=exp(-j*omega*t);

-->plot(t,x2);

-->x2=exp(j*omega*t);

-->plot(t,x2);

-->x2=exp(-j*omega*t);

-->plot(t,x2);

-->xy2=x2*x'

xy2 =

127.99867 - 0.0001310i

-->i

!--error 4

undefined variable : i

-->x2=-sin(omega*t);

-->plot(t,x2)

-->xy2=x2*x'

xy2 =

- 0.0001310

-->